El objetivo está desatendido
El autor lleva sin comentar el objetivo 9 años 2 meses 8 días
Пройти курс "Основы теории графов"
Всем доброго времени суток!
Теория графов довольно полезная и нужная штука, особенно для программистов (которые специалисты, профессионалы, мастера своего дела и т.д. и т.п.). Знаний у меня в ней очень-очень мало, а очень бы хотелось иметь их чуть больше.
Каким-то образом напал на курс "Основы теории графов". Когда я его нашел, он ещё не начался. Так как эта тема мне интересна, знаний мало, а хотелось бы "углубить и расширить" ©, не долго думая подписался на курс. И начал ждать начала.
Начало сего действия было назначено на 12 сентября, т.е. четыре дня назад, на понедельник. Само собой разумеется, мне пришло оповещение. Я зашел, потыкался, прошел самое начало самого начала и из-за загруженности по работе больше туда не заходил.
Но так же нельзя! И поэтому я создаю эту цель и буду двигаться к её окончания прилагая все возможные усилия.
"Наши цели ясны, задачи определены! За работу, товарищи!" ©
P.S. Чуть позже дополню, возможно, описание. А может и нет.
P.P.S. "Please, dear God, don't let me fuck up" ©
Criterio del fin
Курс успешно завершен
Recursos personales
целеустремленность, упертость/упоротость, желание учиться
Lo ecológico del objetivo
Графы очень полезная штука в разработке ПО. И понимание хотя бы основ, IMHO, строго обязательна для любого разработчика, который хочет называть себя профессионалом
-
Основные понятия теории графов - I
Баллы: 22.3 / 25
Задания: 23 / 23
Краткое описание:
Понятие графа. Неориентированный граф. Отношение инцидентности. Петли и мультиребра. Степень вершины. Первая теорема теории графов. Простые графы. Полный и пустой графы. Ориентированный граф. Смежность вершин. Представление графа с помощью структур данных.
Маршрут. Путь. Простой путь. Понятие связности. Компоненты связности. Связность в ориентированном графе. Замкнутый маршрут. Простой цикл. Длина цикла. Обхват графа. Понятие дерева. Двудольные графы. Раскраска вершин графа. Ациклические графы. Топологическая сортировка вершин.
Подграфы. Операции над графами. Удаление ребра. Удаление вершины. Остовный подграф. Индуцированное подмножество вершин. k-фактор. Понятие совершенного паросочетание. Остовный цикл. Мост. Точка сочленения. Операция стягивания ребра. Объединение, пересечение и симметрическая разность графов.
Количество графов на n вершинах. Изоморфизм графа. Непомеченный граф и помеченный граф. Классы эквивалентности. Автоморфизм.
![]()
-
Основные понятия и определения
-
Маршруты, пути, циклы. Понятие связности. Двудольные графы.
-
Подграфы. Основные операции над графами
-
Изоморфизм и автоморфизм графов
-
-
Основные понятия теории графов - II
Баллы: 18 / 24
Задания: 14 / 16
Краткое описание:
Определение дерева. Алгоритм поиска в глубину. Корневое дерево. Уровень и высота дерева. Частично упорядоченное множество. Сравнимые вершины. Нормальное дерево. Перекрестные ребра. Алгоритм поиска в ширину.
Эйлеров путь и цикл. Условия существования эйлерова цикла.
Паросочетание в графе. Совершенное паросочетание. Максимальное паросочетание. Наибольшее по включению паросочетание. "Жадный" алгоритм поиска парасочетания. M-чередующийся путь. M-дополняющий путь. Необходимое и достаточное условие максимальности паросочетания. Теорема Бержа. Поиск паросочетания в двудольном графе. Теорема Холла.
![]()
-
Деревья
-
Эйлеровы графы
-
Паросочетания. Теорема Холла
-
-
Циклы в графах
Баллы: 6.7 / 14
Задания: 8 / 10
Краткое содержание:
Гамильтонов цикл и путь.Формула количества гамильтоновых путей. Теорема Оре. Теорема Дирака.
Графы де Брёйна. Последовательность де Брёйна. Алгоритм построения графа де Брёйна. Гамильтоновы и эйлеровы цикла в графах де Брёйна.
![]()
-
Гамильтоновы циклы
-
Графы Де Брейна
-
-
Связность в графах - 1
Баллы: 16 / 16
Задания: 10 / 10
Краткое содержание:
Вершинная связность. Вершинное разделяющее множество. Вершинно k-связный граф. Реберная связность. Реберное разделяющее множество. Реберно k-связный граф. Реберный разрез.
Похожесть в графе. Компоненты похожести. Построение дерева блоков и точек сочленения 1-связного графа. Вершинный кактус. Реберный кактус. Алгоритм Хопкрофта-Тарьяна.
![]()
-
Вершинная и реберная связность
-
Структура двусвязных графов
-
-
Связность в графах - 2
![]()
-
k-связные графы
-
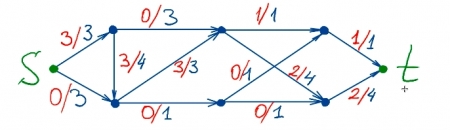
Потоки и сети
-
-
Паросочетания в графах
![]()
-
Независимые множества и покрытия графа
-
Паросочетания в произвольных графах
-
-
Раскраска графов
![]()
-
k-раскрашиваемые графы. Теорема Брукса
-
Нижние оценки на хроматическое число
-
Хроматический многочлен графа
-
-
Планарные графы - 1
![]()
-
Основные свойства планарных графов
-
Формула Эйлера. Карты на поверхностях
-
аскраска планарных графов
-
-
Планарные графы - 2
![]()
-
Критерии планарности графов
-
Карты на поверхностях
-
- 3024
- 15 septiembre 2016, 22:31
¡No omita entradas nuevas!
Suscríbase al objetivo y siga su logro